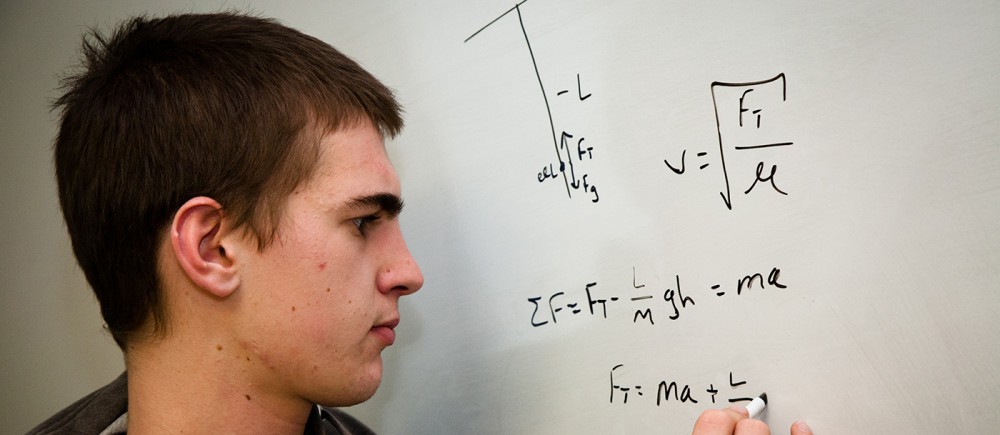Tag Archives: MAA

UML Participation in the 2019 William Lowell Putnam Mathematics Competition

Posted on by
Reply
UML Students working on the Putnam.

What a way to spend your Saturday! Get yourself to campus for 10 AM and work on six math problems for three hours. Then after a two hour break, spend another three hours of six more problems. That’s what thousands of undergraduate students throughout the US and Canada, including 34 UMass Lowell students, did on December 7 to take part in the 2019 William Lowell Putnam Mathematics Competition.

The competition, sponsored by the Mathematical Association of America, took place concurrently throughout the US and Canada. Last year,  4,623 students from 568 institutions participated. There were two 3 hour sessions, each with six problems. As usual, the problems were tough. Here is probably the easiest of them:

Determine all possible values of the expression
A3 +B3 +C3 – 3 A B C,
where A, B, and C are nonnegative integers.

A complete list of problems: 2019 Putnam Problems

Professor Kenneth Levasseur served as supervised competition at UML.   Thanks to the Honors College for providing refreshments for the students on the day of the event.

Results will be announced in late March.

UML Participation in the 2017 Putnam Math Competition

Posted on by

Twenty-six UMass Lowell students competed in the 2017 William Lowell Putnam Mathematics Competition on Saturday, December 2. The competition, sponsored by the Mathematical Association of America, took place concurrently throughout the US and Canada. Last year, 4,164 students from 568 colleges and universities participated. There were two 3 hour sessions, each with six problems. As usual, the problems were tough. Here is one of them:

The 30 edges of a regular icosahedron are distinguished by labeling them 1, 2, …, 30.  How many different ways are there to paint each edge red, white, or blue such that each of the 20 triangular faces of the icosahedron has two edges of the same color and a third edge of a different color?

In case you’ve forgotten, an icosahedron looks like this:

A complete list of problems:  Putnam2017.

Professor Kenneth Levasseur served as supervised competition at UML.   Thanks to the Honors College for providing refreshments for the students on the day of the event.

Results will be announced in late March.