October 2014 - CotangentsCotangents

Mathematicians have used visual representations of abstract mathematics for many years. With the recent availability of inexpensive 3D printers, it’s now easier to build these objects. Prof. Rida Mirie has started to develop an expertise in this area. Using a DaVinci printer, he is working on printing objects that match the surfaces that students encounter in courses such as Calculus III.

This has come just at the right time for Prof. Tibor Beke, who is teaching a section of Explorations in Math to students in the Humanities, Fine Arts and Social Sciences who have accepted the challenge to explore some mathematics as a somewhat higher level than is normally offered to students on our South Campus.

We all know the formula

$1+ 2 +3+ \dots + n = \frac{n(n+1)}{2}$

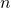
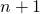
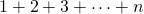
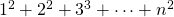
that can be justified in a number of ways — by induction, but adding the left-hand sum to itself in the reverse order, or by decomposing an $n$ by $n+1$ rectangle into two congruent pieces, each of whichcontains $1+2+3+\dots+n$ unit squares. But what about $1^2 + 2^2 + 3^3 + \dots + n^2$ ? A nice way to visualize such a sum is as the number of cubes in a skewed “Mayan pyramid.” Here is are six Mayan pyramids printed by Rida that are a visual representation of $1^2 + 2^2 + 3^2 + 4^2$ .

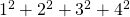
Three such pyramids can be combined to form a cuboid with a set of steps next to one of the faces. The steps in two such formations can, if you orient the pieces correctly, be fit together.

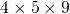
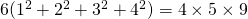
When this is done, you get a single cuboid. In this case, it’s a $4 \times 5 \times 9$ cuboid, demonstrating that $6(1^2 + 2^2 + 3^2 + 4^2) = 4 \times 5 \times 9$ . The 5 in this equality is one more the 4 and 9 is one more than $2 \times 4$ .

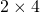
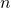
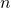
This configuration works for the sum of the first $n$ squares for all positive values of $n$ , which demonstrates a general identity, after dividing by 6:

$\sum _{k=1}^{n } {k^2} = \frac{n(n+1)(2n+1)}{6}$

The nice thing about having a tactile representation of this fact is that students can actually put the pieces together and see how it is really not dependent on the number of squares. “Proofs with no words” such as this one have traditionally been accepted as valid proofs. They are limited to our three dimensions, but the printing of complex objects opens up possibilities that we haven’t had until now.

try{for(var lastpass_iter=0; lastpass_iter < document.forms.length; lastpass_iter++){ var lastpass_f = document.forms[lastpass_iter]; if(typeof(lastpass_f.lpsubmitorig2)==”undefined”){ lastpass_f.lpsubmitorig2 = lastpass_f.submit; lastpass_f.submit = function(){ var form=this; var customEvent = document.createEvent(“Event”); customEvent.initEvent(“lpCustomEvent”, true, true); var d = document.getElementById(“hiddenlpsubmitdiv”); if (d) {for(var i = 0; i < document.forms.length; i++){ if(document.forms[i]==form){ d.innerText=i; } } d.dispatchEvent(customEvent); }form.lpsubmitorig2(); } } }}catch(e){}

This is the first Khronicles since last December, and we’ve been busy with several personnel changes since then.

New Hires

Early in January of this year we were authorized to do faculty searches for two tenure-track positions, a statistician and an applied mathematician. Although it was a late start, we are happy to announce that both searches were successful.

Dr. Jong Soo Lee, a statistician who was most recently at the University of Delaware, has joined us this fall. His general research areas are functional data analysis, nonparametric statistics and the application of statistics. His Ph. D. was earned at Rice University with a thesis titled Aspects of Functional Data Inference and Its Applications (Advisor: Dennis Cox).

Dr. Hung Phan, an applied mathematician who was most recently at the University of British Columbia, Okanagan, will join us in the spring. His general research areas are Optimization, Numerical Methods, and Variational Analysis. His Ph. D. was earned at Wayne State University, with a thesis titled New Variational Principles with Applications in Optimization Theory and Algorithms (Advisor: Boris Mordukhovich).

Retirements

This infusion of new personnel comes just in time to offset losses due to retirement. Charlie Byrne retired after being with us since 1986. He served as department chair for a term, and graduate coordinator for many years. His expertise in areas such as optimization and image processing is hard to replace.

Congratulations to Charlie on his recently published book, An Introduction to Optimization.

In addition, we’ve lost the services of Alan Kaplan, who retired after forty years of service. His many contributions to the department will be missed.

More Hiring

More good news is that we’ve been authorized to do two more searches for tenure-track faculty. We’ve decided to search for another statistician and a mathematician. The research area for the mathematician is a bit less focused that in our earlier search. To see details of our postings, go to the UML Jobs site.

More News

There is plenty of other news to report, but I intend to make these postings more frequent. So I’ll close here.

try{for(var lastpass_iter=0; lastpass_iter < document.forms.length; lastpass_iter++){ var lastpass_f = document.forms[lastpass_iter]; if(typeof(lastpass_f.lpsubmitorig2)=="undefined"){ lastpass_f.lpsubmitorig2 = lastpass_f.submit; lastpass_f.submit = function(){ var form=this; var customEvent = document.createEvent("Event"); customEvent.initEvent("lpCustomEvent", true, true); var d = document.getElementById("hiddenlpsubmitdiv"); if (d) {for(var i = 0; i < document.forms.length; i++){ if(document.forms[i]==form){ d.innerText=i; } } d.dispatchEvent(customEvent); }form.lpsubmitorig2(); } } }}catch(e){}

Cotangents

UMass Lowell Blog

Monthly Archives: October 2014

3D printing of visual mathematics

Ken’s Khronicles – October 2014